Another class of effective learning methods for the ![]() -armed bandit
problem are pursuit methods. Pursuit methods maintain both
action-value estimates and action preferences, with the preferences
continually "pursuing" the action that is greedy according to the
current action-value estimates. In the simplest pursuit method, the action
preferences are the probabilities,
-armed bandit
problem are pursuit methods. Pursuit methods maintain both
action-value estimates and action preferences, with the preferences
continually "pursuing" the action that is greedy according to the
current action-value estimates. In the simplest pursuit method, the action
preferences are the probabilities, ![]() , with which each action,
, with which each action, ![]() , is
selected on play
, is
selected on play ![]() .
.
After each play, the probabilities are updated so as to
make the greedy action more likely to be selected. After the ![]() th play, let
th play, let
![]() denote the greedy action (or a random sample
from the greedy actions if there are more than one) for the (
denote the greedy action (or a random sample
from the greedy actions if there are more than one) for the (![]() )st play. Then
the probability of selecting
)st play. Then
the probability of selecting ![]() is incremented a fraction,
is incremented a fraction, ![]() , of the way toward 1:
, of the way toward 1:
|
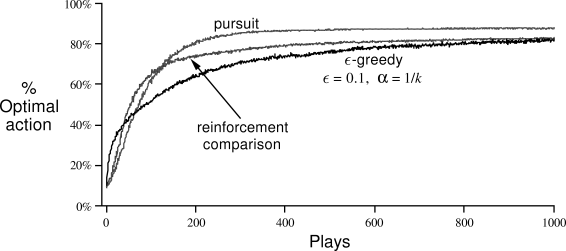
Figure
2.6 shows the performance of the pursuit algorithm described
above when the action values are estimated using sample averages (incrementally
computed using ![]() ). In these results, the initial action
probabilities were
). In these results, the initial action
probabilities were
![]() , for all
, for all ![]() , and the parameter
, and the parameter ![]() was 0.01. For
comparison, we also show the performance of an
was 0.01. For
comparison, we also show the performance of an
![]() -greedy method (
-greedy method (![]() ) with action values also estimated using
sample averages. The performance of the reinforcement comparison algorithm from
the previous section is also shown. Although the pursuit algorithm performs the
best of these three on this task at these parameter settings, the ordering could
well be different in other cases. All three of these methods appear to have their
uses and advantages.
) with action values also estimated using
sample averages. The performance of the reinforcement comparison algorithm from
the previous section is also shown. Although the pursuit algorithm performs the
best of these three on this task at these parameter settings, the ordering could
well be different in other cases. All three of these methods appear to have their
uses and advantages.
Exercise 2.12 An
Exercise 2.13 For many of the problems we will encounter later in this book it is not feasible to update action probabilities directly. To use pursuit methods in these cases it is necessary to modify them to use action preferences that are not probabilities but that determine action probabilities according to a softmax relationship such as the Gibbs distribution (2.9). How can the pursuit algorithm described above be modified to be used in this way? Specify a complete algorithm, including the equations for action values, preferences, and probabilities at each play.
Exercise 2.14 (programming) How well does the algorithm you proposed in Exercise 2.13 perform? Design and run an experiment assessing the performance of your method. Discuss the role of parameter settings in your experiment.
Exercise 2.15 The pursuit algorithm described above is suited only for stationary environments because the action probabilities converge, albeit slowly, to certainty. How could you combine the pursuit idea with the