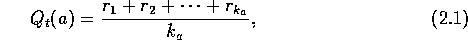



The action-value methods we have discussed so far all estimate their action values as the sample averages of observed rewards. The obvious implementation is to maintain, for each action, a, a record of all the rewards that have followed the selection of that action. Then, whenever estimate of the action value is needed, it can be computed according to (2.1), which we repeat here:
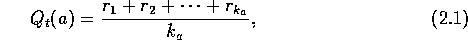
where 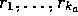 are all the rewards received
following all selections of action a up until play t. A problem with this
straightforward implementation is that its memory and computational requirements grow
over time without bound. That is, each additional reward following a selection of
action a requires more memory to store it and results in more computation being
required to compute
are all the rewards received
following all selections of action a up until play t. A problem with this
straightforward implementation is that its memory and computational requirements grow
over time without bound. That is, each additional reward following a selection of
action a requires more memory to store it and results in more computation being
required to compute 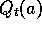 .
.
As you might suspect, this is not really necessary. It is easy to devise
incremental update formulas for computing averages with small, constant
computation required to process each new reward. For some action, let 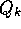 denote
the average of its first k rewards. Given this average and a
denote
the average of its first k rewards. Given this average and a 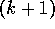 st reward,
st reward,
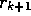 , the average of all k+1 rewards can be computed by:
, the average of all k+1 rewards can be computed by:
which holds even for k=0, obtaining 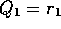 for arbitrary
for arbitrary 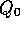 . This
implementation requires memory only for
. This
implementation requires memory only for 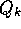 and k, and only the small
computation (2.4) for each new reward.
and k, and only the small
computation (2.4) for each new reward.
The update rule (2.4) is of a form that occurs frequently throughout this book. The general form is:
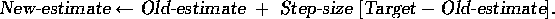
The expression 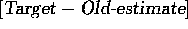 is an
error in the estimate. It is reduced by taking a step toward the
``target". The target is presumed to indicate a desirable direction in
which to move, though it may be noisy. In the case above, for example,
the target is the
is an
error in the estimate. It is reduced by taking a step toward the
``target". The target is presumed to indicate a desirable direction in
which to move, though it may be noisy. In the case above, for example,
the target is the
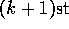 reward.
reward.
Note that the step size used in the incremental method described above changes from
time step to time step. In processing the kth reward for action a, that method
uses a step-size of 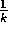 . In this book we denote the step size by the
symbol
. In this book we denote the step size by the
symbol 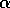 , or, more generally, by
, or, more generally, by 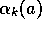 . For example, the above incremental
implementation of the sample average method is described by the equation
. For example, the above incremental
implementation of the sample average method is described by the equation
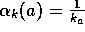 . Accordingly, we sometimes use the informal shorthand
. Accordingly, we sometimes use the informal shorthand
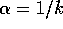 to refer to this case, leaving the action dependence implicit.
to refer to this case, leaving the action dependence implicit.
Exercise  .
.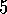
Give pseudo-code for a complete algorithm for the n
-armed bandit problem.
Use greedy action selection and incremental computation of
action values with 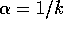 step size. Assume a function
step size. Assume a function 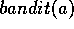 that takes an
action and returns a reward. Use arrays and variables; do not subscript anything by
the time index t. Indicate how the action values are initialized and
updated after each reward.
that takes an
action and returns a reward. Use arrays and variables; do not subscript anything by
the time index t. Indicate how the action values are initialized and
updated after each reward.


